이번에 프로그래머스에서 공채 코댕 대비 코딩 테스트 실전 모의고사라는 느낌으로 문제를 출제했습니다!
3 문제 이고, 2시간 반의 시험 시간을 가졌죠!
생각보다 난이도가 쉬웠지만, 역시 생각보다 푸는 시간이 늦었네요 ㅋㅋㅋㅋ
그럼, 1번 부터 한 번 풀이를 시작하게씁니다!
참고로, 제가 푼 방법 말고도 공식적인 해설이 궁금하시다면, 여기를 가보세용!
1번 팰린드롬
문제 설명
앞에서부터 읽을 때와 뒤에서부터 읽을 때 똑같은 단어를 팰린드롬(palindrome)이라고 합니다. 예를들어서 racecar, 10201은 팰린드롬 입니다.
두 자연수 n, m이 매개변수로 주어질 때, n 이상 m 이하의 자연수 중 팰린드롬인 숫자의 개수를 return 하도록 solution 함수를 완성해 주세요.
제한사항
- m은 500,000이하의 자연수이며, n은 m 이하의 자연수입니다.
입출력 예
| n | m | result |
|---|---|---|
| 1 | 100 | 18 |
| 100 | 300 | 20 |
입출력 예 설명
입출력 예 #1
1 이상 100 이하의 팰린드롬은 다음과 같이 18개가 있습니다.
1, 2, 3, 4, 5, 6, 7, 8, 9, 11, 22, 33, 44, 55, 66, 77, 88, 99
입출력 예 #2
100 이상 300 이하의 팰린드롬은 다음과 같이 20개가 있습니다.
101, 111, 121, 131, 141, 151, 161, 171, 181, 191, 202, 212, 222, 232, 242, 252, 262, 272, 282, 292
어떻게 풀까?
n 부터 m까지 펠린드롬인 수를 찾는 것 입니다!
정말 직관적이게, n을 스트링으로 만들어서, 펠린드롬인지 아닌지 확인해보는 방법을 이용합시다.
펠린드롬인지는, i번째 수와 끝에있는 글자 - i 번째 수가 같은지 계속 비교하면 됩니다!
펠린드롬이면 결과값에 1을 더해주고, 마지막에 결과값을 return 해주면 됩니다.
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 | #include <string> #include <vector> #include <iostream> #include<string> using namespace std; //int를 숫자 스트링으로 만듬 string toString(int n){ string res; while(n){ res.push_back((n%10) + '0'); n /= 10; } return res; } int res = 0; //앞 뒤가 같은지 확인 bool isPelin(string& str){ int len = str.size(); for(int i = 0; i < len/2; i++){ if(str[i] != str[len-1-i]) return false; } return true; } int solution(int n, int m) { int answer = 0; //n부터 m까지 숫자를 스트링으로 만들고, 펠린드롬 검사 for(int i = n; i <= m; i++){ string str = toString(i); answer += isPelin(str); } return answer; } | cs |
시간 복잡도
n부터 m까지 한번씩 확인하고, 자리수는 생각보다 많지 않기 때문에, 시간복잡도는 O(N)이 됩니다!
2번 배상비용 최소화
문제 설명
OO 조선소에서는 태풍으로 인한 작업지연으로 수주한 선박들을 기한 내에 완성하지 못할 것이 예상됩니다. 기한 내에 완성하지 못하면 손해 배상을 해야 하므로 남은 일의 작업량을 숫자로 매기고 배상비용을 최소화하는 방법을 찾으려고 합니다.
배상 비용은 각 선박의 완성까지 남은 일의 작업량을 제곱하여 모두 더한 값이 됩니다.
조선소에서는 1시간 동안 남은 일 중 하나를 골라 작업량 1만큼 처리할 수 있습니다. 조선소에서 작업할 수 있는 N 시간과 각 일에 대한 작업량이 담긴 배열(works)이 있을 때 배상 비용을 최소화한 결과를 반환하는 함수를 만들어 주세요. 예를 들어, N=4일 때, 선박별로 남은 일의 작업량이 works = [4, 3, 3]이라면 배상 비용을 최소화하기 위해 일을 한 결과는 [2, 2, 2]가 되고 배상 비용은 22 + 22 + 22 = 12가 되어 12를 반환해 줍니다.
제한사항
- 일할 수 있는 시간 N : 1,000,000 이하의 자연수
- 배열 works의 크기 : 1,000 이하의 자연수
- 각 일에 대한 작업량 : 1,000 이하의 자연수
입출력 예
| N | works | result |
|---|---|---|
| 4 | [4,3,3] | 12 |
| 2 | [3,3,3] | 17 |
입출력 예 설명
입출력 예 #1
문제의 예제와 같습니다.
입출력 예 #2
배상 비용을 최소화하기 위해 일을 한 결과는 [2, 2, 3]가 되고 배상 비용은 22 + 22 + 32 = 17가 되어 17를 반환해 줍니다.
어떻게 풀까?
실은, 가장 많이 고민했던 문제입니다.
가장 먼저 깨달아야 하는 사실은, 언제 배상 비용이 최소화 되는가? 입니다.
개인적으로 수학적으로 증명하기가 굉~장히 어렵지만..
어쨌든, 가장 많이 남은 작업시간을 먼저 처리하는 것이 배상 비용을 최소로 만들 수 있습니다.
그렇다는 말은, 선박들의 남은 작업량들을 h 이하로 동일하게 맞춰야 한다는 것이죠!
그럼! 이제 생각해봅시다!
배상 비용은 남은 작업량의 제곱들의 합 입니다!
그리고, h를 구하면, 작업해야 하는 일의 양과 남은 일의 양을 동시에 알 수 있습니다!
위의 그림을 예로 들어보겠습니다!
총 작업량은 4와 1 입니다!
이 때, 모든 작업량 3 이하로 맞춰야 하는 경우를 생각해 봅시다.
작업량 4는 작업량 3으로 맞추기 위해서
1의 작업을 해야합니다!
그리고 남은 작업량은 4-1 = 3이죠!
작업량 1은 어짜피 3 이하이기 때문에 추가 작업이 필요없습니다!
그리고 남은 작업량은 1이죠!
이렇게 되면, 남은 작업량이 3과 1이기 때문에, 배상 비용은 10 이 됩니다!
자! 이렇게 보면
배상 비용은 h가 낮아질수록 줄어드는 것을 알 수 있죠!
반대로, h가 낮아질수록 해야하는 작업량은 많아 집니다!
문제에서는 할 수 있는 작업량을 주기 때문에, 이 할 수 있는 작업량을 통해서 가능한 가장 낮은 h값을 찾을 수 있습니다!
가장 높은 h값부터 시작해서, h를 점점 낮춰가면서 필요한 작업량이 할 수 있는 작업량을 넘는 부분 바로 이전이 최소의 배상 비용을 가지는 h값 이라는 것이죠!
아직 이해가 잘 안되신다면, 문제를 푸는 과정을 그림으로 설명해드리겠습니다.
예시는 첫 번째 테스트 케이스인,
4 [4, 3, 3] 으로 설명해 드리겠습니다!
일할 수 있는 시간 : 4
0번 선박의 남은 작업량 : 4
1번 선박의 남은 작업량 : 3
2번 선박의 남은 작업량 : 3
우선, h를 작업량의 최대 높이인 4로 맞춰봅니다!
이렇게 맞추면, 0번 선박과 1번 선박, 2번 선박 모두 4 이하이기 때문에, 최대 높이를 4로 맞출 때 일할 수 있는 시간은 4시간이 남습니다.
h를 3으로 맞춰 봅시다.
그렇다면, 선박 0의 작업량은 4이기 때문에, 1시간을 잘라내야 합니다.
하지만, 일할 수 있는 시간은 4 시간이기 때문에 전혀 문제가 생기지 않습니다.
h를 2로 맞춰 봅시다.
위와 같은 방식을 쓰면, 작업해야하는 량은 4가 됩니다.
일할 수 있는 시간은 4 이기 때문에, 다행히도 문제가 생기지 않습니다!
높이를 1로 맞추면 어떻게 될까요?
작업해야 하는 시간은 총 7시간이 됩니다.
일할 수 있는 시간이 4시간이기 때문에, 모든 남은 작업량을 1 이하로 맞추는 것은 불가능 합니다!
즉, 최소의 배상 비용을 가지는 높이는 2로 맞춰야 합니다!
이렇게, 배상 비용을 맞추면, 답은
가 됩니다!
다만, 생각해봐야할 경우가 2 가지 더 있습니다.
1번 케이스를 살짝 바꿔 봅시다!
만약 일할 수 있는 시간이 4가 아니라 5 였다면 어떨까요???
마찬가지로 4이기 때문에 h는 2가 될 수 있습니다.
하지만, h는 1이 될수가 없죠.
높이를 2로 맞추긴 하지만, 일할 수 있는 시간이 1 남습니다!
이 일할 수 있는 시간이 남기 때문에, 당연히 작업을 한 번 해줘야 합니다.
그러면, 2 2 2의 높이에서 한 시간 일을 더 해줘야 겠죠!
그리고, 배상 비용은
가 됩니다.
이렇게, 추가적으로 남는 시간을 빼주시면 완벽한 답이 됩니다!
다만, 이러한 경우는 또 어떨까요????
어떤 답의 h가 다음과 같은 경우 입니다!
맨 처음에, 작업량이 많은 순으로 작업을 먼저 시행해야 최선이 된다고 했습니다!
작업량이 많은 순으로 한 번 처리하고, 이 처리한 작업을 또 정렬해서, 아직 가장 해야할 일이 많은 작업의 일을 처리해야 합니다.
어떤 저장소에서 하나의 원소의 값을 뺄 때 항상 큰 값을 얻어야하고, 이 수를 처리한 다음에 다시 삽입을 하는 연산이 많습니다!
따라서, 한 수의 삽입이 빠르고, 가장 큰 값을 뺄 때의 연산이 빠른 우선 순위 큐를 사용합시다!
즉, 남은 작업량을 h이하로 맞춘 후에, 우선순위 큐에 남은 작업량들을 모두 넣습니다.
이제 우선순위 큐에서 숫자를 하나 빼면, 이 수가 가장 작업량이 많은 수 일 것입니다!
이제 이 수에서 1을 빼고, 추가로 할 수 있는 작업량도 1 뺀 다음에 그 수를 우선순위 큐에 넣는 과정을 추가 작업량이 0이 될 때까지 반복하면 됩니다!
이 예제에서는 추가로 일할 수 있는 시간 2개는 4를 하나 깎고, 3을 하나 깎는 다음과 같은 모습이 되겠죠!
문제에서 h는 1000이 넘지 않기 때문에 1000부터 선형적으로 빼주면서 h값을 구해줘도 되지만,
훨씬 효율적인 계산을 위해 파라메트릭 서치를 이용해서 코드를 짜 보았습니다!
왜냐하면, h 이상의 값은 모두 처리가 가능한 값이고, h 미만의 값은 모두 처리가 불가능한 값이기 때문입니다!
하나의 기준점에 대한 답을 결정하면, 그 이전이나, 그 다음에 해당하는 값도 모두 결정할 수 있죠!
결국 찾아야 하는것은 작업을 했을 때, 남은 작업량이 0 이상이 되게 하는 수 중 가장 작은 수를 구하는 것이기 때문에, 파라메트릭 서치를 이용할 수 있습니다!
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 | #include<vector> #include<iostream> #include<algorithm> #include<functional> #include<queue> using namespace std; //조건 (모든 works의 높이를 h로 만들 수 있는가?) bool canConstruct(int no, vector<int>& works, int h) { for (int i = 0; i < works.size(); i++) { int minus = works[i] < h ? 0 : works[i] - h; no -= minus; } return no >= 0; } //파라메트릭 서치(만들 수 있는 높이들 중에 최고점) int bs(int no, vector<int>& works) { int l = 0, r = 1000; while (l <= r) { int m = (l + r) / 2; if (!canConstruct(no, works, m)) { l = m + 1; } else { r = m - 1; } } //l이 만들 수 있는 점들의 최고 높이이다. return l; } int solution(int no, vector<int> works) { sort(works.begin(), works.end(), greater<int>()); int answer = 0; //(파라메트릭 서치 방식) int h = bs(no, works); //높이가 최개 1천이기 때문에 그냥 1부터 풀어도 된다.(선형) /* int h = 1000;// = bs(no,works); for(int i = 1000; i >=0; i--){ if(canConstruct(no,works, i)){ h = i; } else break; } */ priority_queue<int> pq; //만들 수 있는 높이에서 work 들의 길이가 몇이 되고, no는 얼마나 남는지 계산 for (int i = 0; i < works.size(); i++) { int minus = works[i] < h ? 0 : works[i] - h; works[i] = h < works[i] ? h : works[i]; pq.push(works[i]); no -= minus; } //남은 것이 많으면 pq에서 높은 것 부터 제거 while (no) { int now = pq.top(); pq.pop(); now--; no--; pq.push(now); } //이제 남은 work들의 제곱을 더해주면 끝 while (pq.size()) { answer += pq.top()*pq.top(); pq.pop(); } return answer; } | cs |
시간 복잡도
파라메트릭 서치를 썼기 때문에, 시간 복잡도는 입니다.
(h는 최대의 작업량 입니다! 여기서는 1000 이군요!)
3번 버스 여행
문제 설명
버스정류장 N개가 있습니다. 각 정류장에는 1번부터 N번까지의 번호가 매겨져 있습니다. 2차원 배열로 주어진 정류장 표지판(signs)에는 A번 정류장에서 B번 정류장으로 가는 버스가 있다면 1, 없다면 0으로 표시되어 있습니다.
예를 들어, 3개의 버스정류장이 있을 때

로 표시된 정류장 표지판이 주어진다면,
- 1번 정류장에서 2번 정류장으로 갈 수 있습니다. (A=1, B=2)
- 2번 정류장에서 3번 정류장으로 갈 수 있습니다. (A=2, B=3)
- 3번 정류장에서 1번 정류장으로 갈 수 있습니다. (A=3, B=1)
또한, 버스를 갈아타는 것이 가능합니다. 예를 들어, 위 예시에서는 1번에서 2번 정류장으로, 그리고 2번에서 3번 정류장으로 가는 버스가 있으므로, 한 번 갈아타서 1번에서 3번 정류장으로 갈 수 있습니다. 버스는 여러번 갈아타는 것이 가능합니다.
우리는 이 표를 이용해서 특정 정류장 A에서 특정 정류장 B로 갈 수 있는지 판단하여, 갈 수 있으면 1, 갈 수 없으면 0으로 표시하려고 합니다.
위 예시에서는
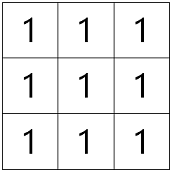
이 되며. A번째 줄의 B번째 숫자는 A 정류장에서 B 정류장으로 갈 수 있는 지의 정보를 나타냅니다. 단, 출발지와 목적지 사이에서 적어도 하나의 버스를 타는 경우에만 1로 표시합니다.
정류장 표지판(signs)이 매개변수로 주어질 때, 특정 정류장 A에서 특정 정류장 B로 도달할 수 있는지를 표시하여 return 하는 solution 함수를 완성해 주세요. 위 예시의 경우는 [[1,1,1],[1,1,1],[1,1,1]]로 return 하면 됩니다.
제한사항
- N : 100 이하의 자연수
- 정류장 표지판(signs)는 2차원 배열이며, 1 또는 0으로만 이루어져 있습니다. 단, i번째 줄의 i번째 숫자는 항상 0입니다.
입출력 예
| n | signs | answer |
|---|---|---|
| 3 | [[0,1,0],[0,0,1],[1,0,0]] | [[1,1,1],[1,1,1],[1,1,1]] |
| 3 | [[0,0,1],[0,0,1],[0,1,0]] | [[0,1,1],[0,1,1],[0,1,1]] |
입출력 예 설명
입출력 예 #1
문제의 예시와 같습니다.
입출력 예 #2
- 1번 정류장->3번 정류장->2번 정류장으로 갈 수 있으므로, 1행은 [0,1,1]이 됩니다.
- 2번 정류장->3번 정류장->2번 정류장으로 갈 수 있으므로, 2행은 [0,1,1]이 됩니다.
- 3번 정류장->2번 정류장->3번 정류장으로 갈 수 있으므로, 3행은 [0,1,1]이 됩니다
어떻게 풀까?
n이 100이고, 모든 쌍에 대한 이동 가능 여부를 구하는 문제군요.
플로이드-와샬을 써도 충분히 풀 수 있습니다.
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 | #include <iostream> #include<vector> using namespace std; vector<vector<int> > solution(int n, vector<vector<int> > signs) { //플로이드-와샬 for(int k = 0; k < n; k++){ for(int i = 0; i < n; i++){ for(int j = 0; j < n; j++){ signs[i][j] |= signs[i][k] && signs[k][j]; } } } return signs; } | cs |
시간 복잡도
플로이드 와샬은 의 시간 복잡도를 가집니다!
for 문이 3개가 겹치는 것을 보고 알 수 있죠!
여담
2번 문제가 높이가 굉장히 큰 줄 알았는데, 알고보니 할 수 있는 작업량이 큰 것이었어요!
그래서 파라메트릭 서치로 풀었는데, 그래서 굉장히 오래걸렸답니다.
생각보다 어려운 수준으로는 안나와서 시간 내에 다 풀 수 있었어요!
그래도... 꽤 늦게 푼 느낌이 없지 않아 있네요 흑.. 1번 3번은 굉장히 빨리 풀었지만 말이에요!
그래도, 이번 파라메트릭 구현을 통해서 파라메트릭 서치가 얼마나 구현이 귀찮은지 다시 한 번 깨달을 수 있었어요. ㄷㄷㄷ
진짜 파라메트릭 서치는 많이 구현해봐야 할 것 같아요.. 자꾸 인덱스 1차이 나게 리턴되서 힘들었어요.









