[Codeforces] Codeforces Round #505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final)

3번 째 코포 글입니다.

으아... 이전에 풀었던거 복기하려고 하니 정말 미치겠네용

기억이 잘 안나서 포스팅 하는데도 더 시간이 많이 걸리는 것 같아요.

어쩄든, 다시 시작합니다! 후욱.. 이거 말고도 2개 남았어요 흑흑...

Panic is rising in the committee for doggo standardization — the puppies of the new brood have been born multi-colored! In total there are 26 possible colors of puppies in the nature and they are denoted by letters from 'a' to 'z' inclusive.

The committee rules strictly prohibit even the smallest diversity between doggos and hence all the puppies should be of the same color. Thus Slava, the committee employee, has been assigned the task to recolor some puppies into other colors in order to eliminate the difference and make all the puppies have one common color.

Unfortunately, due to bureaucratic reasons and restricted budget, there's only one operation Slava can perform: he can choose a color $x$ such that there are currently at least two puppies of color $x$ and recolor all puppies of the color $x$ into some arbitrary color $y$ . Luckily, this operation can be applied multiple times (including zero).

For example, if the number of puppies is $7$ and their colors are represented as the string "abababc", then in one operation Slava can get the results "zbzbzbc", "bbbbbbc", "aaaaaac", "acacacc" and others. However, if the current color sequence is "abababc", then he can't choose $x$ ='c' right now, because currently only one puppy has the color 'c'.

Help Slava and the committee determine whether it is possible to standardize all the puppies, i.e. after Slava's operations all the puppies should have the same color.

Input

The first line contains a single integer $n$ ( $1 \leq n \leq 10^{5}$ ) — the number of puppies.

The second line contains a string $s$ of length $n$ consisting of lowercase Latin letters, where the $i$ -th symbol denotes the $i$ -th puppy's color.

Output

If it's possible to recolor all puppies into one color, print "Yes".

Otherwise print "No".

Output the answer without quotation signs.

Examples
inputCopy
6
aabddc
outputCopy
Yes
inputCopy
3
abc
outputCopy
No
inputCopy
3
jjj
outputCopy
Yes

Note

In the first example Slava can perform the following steps:

take all puppies of color 'a' (a total of two) and recolor them into 'b';
take all puppies of color 'd' (a total of two) and recolor them into 'c';
take all puppies of color 'b' (three puppies for now) and recolor them into 'c'.

In the second example it's impossible to recolor any of the puppies.

In the third example all the puppies' colors are the same; thus there's no need to recolor anything.

문제 해석

어렵게 설명해놨지만, 한 문자열에서 글자가 2개가 있으면, 해당 글자는 아무렇게나 바꿔버릴 수 있습니다.

이를 '도고'라고 합니다.

도고는 여러번 적용할 수 있고, 심지어 0번 적용할 수도 있습니다.

이 때, 모든 컬러를 똑같게 할 수 있는지 묻는 문제입니다.

어떻게 풀까?

어떤 문자가 2개 이상 이라고 해봅시다.

그러면, 이 2개의 문자는 다른색으로 변경할 수 있습니다.

그 문자는 또 다시 2개 이상이죠!

한 마디로, 2개 이상인 문자가 하나라도 있다면, 해당 문제는 무조건 똑같은 색으로 만들어 버릴 수 있는 것입니다!!

단, 한 문자일때는 무조건 Yes겠죠!

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#pragma once
#include<cstdio>
int nums[256];
int main() {
    int n;
    scanf("%d\n", &n);
    if (n == 1) {
        printf("Yes\n");
        return 0;
    }
    bool res = false;
    for (int i = 0; i < n; i++) {
        char a;
        scanf("%c\n", &a);
        nums[a]++;
        if (nums[a] == 2)
        {
            res = true;
        }
    }
    res ? printf("Yes\n") : printf("No\n");
    return 0;
}
Colored by Color Scripter
cs

시간 복잡도

시간 복잡도는 모든 문자열에서 문자가 2개가 나오는지 확인해야 하기 때문에 O(N)입니다.

During the research on properties of the greatest common divisor (GCD) of a set of numbers, Ildar, a famous mathematician, introduced a brand new concept of the weakened common divisor (WCD) of a list of pairs of integers.

For a given list of pairs of integers $(a_{1}, b_{1})$ , $(a_{2}, b_{2})$ , ..., $(a_{n}, b_{n})$ their WCD is arbitrary integer greater than $1$ , such that it divides at least one element in each pair. WCD may not exist for some lists.

For example, if the list looks like $[(12, 15), (25, 18), (10, 24)]$ , then their WCD can be equal to $2$ , $3$ , $5$ or $6$ (each of these numbers is strictly greater than $1$ and divides at least one number in each pair).

You're currently pursuing your PhD degree under Ildar's mentorship, and that's why this problem was delegated to you. Your task is to calculate WCD efficiently.

Input

The first line contains a single integer $n$ ( $1 \leq n \leq 150 000$ ) — the number of pairs.

Each of the next $n$ lines contains two integer values $a_{i}$ , $b_{i}$ ( $2 \leq a_{i}, b_{i} \leq 2 \cdot 10^{9}$ ).

Output

Print a single integer — the WCD of the set of pairs.

If there are multiple possible answers, output any; if there is no answer, print $- 1$ .

Examples
inputCopy
3
17 18
15 24
12 15
outputCopy
6
inputCopy
2
10 16
7 17
outputCopy
-1
inputCopy
5
90 108
45 105
75 40
165 175
33 30
outputCopy
5

Note

In the first example the answer is $6$ since it divides $18$ from the first pair, $24$ from the second and $12$ from the third ones. Note that other valid answers will also be accepted.

In the second example there are no integers greater than $1$ satisfying the conditions.

In the third example one of the possible answers is $5$ . Note that, for example, $15$ is also allowed, but it's not necessary to maximize the output.

문제 해석

WCD라는 것을 정의했습니다!

두 수 (a,b)가 있고,

이 쌍이 n개가 있습니다.

WCD는 2 개의 쌍 들중에서 딱 하나씩을 골랐을 때, WCD로 나눠지는 수 중에서 1이 아닌 수 입니다!

예를들면,

(12, 15)

(25, 18)

(10, 24)

의 WCD는 2,3,5,6 입니다!

를 고르면, 2,3,6의 수들이 위 수들과 나눠질 수 있고,

15,

25,

을 고르면, 5가 위 수들과 나눠질 수 있기 때문입니다!

이 때, N과 N개의 두 쌍이 주어졌을때, WCD 아무거나 하나를 출력하면 됩니다!

어떻게 풀까?

우선, 가장 중요한 것은 두 쌍이 공용하고 있는 수와 공용하지 않는 수를 모두 포함하는게 좋다고 생각했습니다!

즉, 최소 공배수를 이용하는 것이죠!

제가 생각한 방법은 이렇습니다!

일단, WCD는 1이 아닌 약수를 구하는 것 입니다!

그리고, 쌍 (a,b)에서 a 또는 b 둘중 하나에만 속하는 약수이면 되죠!

즉, n-1번째 쌍까지 올 수 있는 WCD가 존재한다고 치면,

n번째 WCD를 구할 때에는,

n-1번쨰 WCD들 후보들과 a의 약수들의 교집합,

그리고 n-1번째 WCD 후보들과 b의 약수들의 교집합을 합집합 한 것이죠!

이렇게 정리하니까 뭔가 방법이 보입니다!

이전의 WCD 후보들은 다시말하면, WCD 후보들의 최소 공배수 라는 의미이죠!

이전의 WCD 후보들과 a의 약수들의 교집합은 즉, GCD(WCD, a)이고,

WCD 후보들과 b의 약수들의 교집합은 GCD(WCD, b)이겠죠!

그리고 이들을 이용하여 n번째 WCD 후보들은 GCD(WCD, a)와 GCD(WCD, b)의 합집합인 최소 공배수를 구하면 됩니다!!!

이렇게 하면, 이전의 WCD 후보들 중에서 a또는 b에 없는 약수들을 버림과 동시에, WCD들 후보중에서 a에 속하기만 하는 약수와, WCD들의 후보들 중에서 b에 속하는 약수들을 모두 가져올 수 있는 것이죠!

하지만, 이렇게 마지막에 이 값을 출력해서는 안됩니다!

왜냐하면, 마지막에는 마지막 쌍들의 WCD 후보에 a와 b의 합집합이 된 상태이기 때문이죠!

마지막 쌍의 a가 포함하고 있는 약수를, 이전 쌍에서는 포함하고 있지 않을 수도 있죠.

때문에, 정확한 WCD를 구하기 위해서는 구해진 WCD후보들을

다시 처음부터 a 또는 b와 최대 공약수를 구해서 1이 아닌 값을 구해 나가면 됩니다!

이렇게 마지막에 구해진 값이 1 이라면 -1을 출력하고, 1이 아니라면 그 수를 그대로 출력하면 됩니다!

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
 
 #pragma once
#include<cstdio>
long long pa[150000][2],n;
 
long long GCD(long long a, long long b) {
    if(a < b){
        long long temp = a;
        a = b;
        b = temp;
    }
 
    while (b) {
        long long r = a % b;
        a = b;
        b = r;
    }
    return a;
}
 
int main() {
    scanf("%d\n", &n);
    scanf("%lld %lld\n", &pa[0][0], &pa[0][1]);
 
    long long lcm;
 
    long long gcd = GCD(pa[0][0], pa[0][1]);
    lcm = pa[0][0] * pa[0][1] / gcd;
 
    for (int i = 1; i < n; i++) {
        scanf("%lld %lld\n", &pa[i][0], &pa[i][1]);
 
        long long gcds[2] = { GCD(pa[i][0], lcm), GCD(pa[i][1], lcm) };
        gcd = GCD(gcds[0], gcds[1]);
 
        lcm = gcds[0]*gcds[1]/gcd;
        if (lcm == 1) {
            printf("-1\n");
            return 0;
        }
    }
    for (int i = 0; i < n; i++) {
        long long temp = GCD(lcm, pa[i][0]);
        if (temp == 1) {
            temp = GCD(lcm, pa[i][1]);
        }
 
        lcm = temp;
    }
    printf("%lld\n", lcm);
    return 0;
}
Colored by Color Scripter
cs

시간 복잡도

시간 복잡도는 O(N) 입니다!

Is there anything better than going to the zoo after a tiresome week at work? No wonder Grisha feels the same while spending the entire weekend accompanied by pretty striped zebras.

Inspired by this adventure and an accidentally found plasticine pack (represented as a sequence of black and white stripes), Grisha now wants to select several consequent (contiguous) pieces of alternating colors to create a zebra. Let's call the number of selected pieces the length of the zebra.

Before assembling the zebra Grisha can make the following operation $0$ or more times. He splits the sequence in some place into two parts, then reverses each of them and sticks them together again. For example, if Grisha has pieces in the order "bwbbw" (here 'b' denotes a black strip, and 'w' denotes a white strip), then he can split the sequence as bw|bbw (here the vertical bar represents the cut), reverse both parts and obtain "wbwbb".

Determine the maximum possible length of the zebra that Grisha can produce.

Input

The only line contains a string $s$ ( $1 \leq | s | \leq 10^{5}$ , where $| s |$ denotes the length of the string $s$ ) comprised of lowercase English letters 'b' and 'w' only, where 'w' denotes a white piece and 'b' denotes a black piece.

Output

Print a single integer — the maximum possible zebra length.

Examples
inputCopy
bwwwbwwbw
outputCopy
5
inputCopy
bwwbwwb
outputCopy
3

Note

In the first example one of the possible sequence of operations is bwwwbww|bw $\to$ w|wbwwwbwb $\to$ wbwbwwwbw, that gives the answer equal to $5$ .

In the second example no operation can increase the answer.

문제 해석

어떤 문자열이 주어집니다.

해당 문자열은 i번째에서 문자열을 두 부분으로 나눌 수 있습니다.

나눠진 두 부분을 역순으로 바꿔서 다시 합칩니다!

예를들어, bwbbw는 bw | bbw 로 나눌 수 있고, 이를 거꾸로하면 wb | wbb 가 됩니다.

즉, wbwbb라는 글자를 만들 수 있습니다!

이러한 연산을 0번부터 계속 할 수 있을 때, 교차되는 w와 b가 교차되는 최고의 길이를 출력하면 됩니다!

어떻게 풀까?

이 문제는 w와 b로 봐서는 풀이가 잘 보이지 않는 문제입니다.

대신, 인덱스로 보겠습니다!!

123456 입니다.

123 | 456 으로 나눠 봅시다.

321654 가 됩니다!

이번엔 32 | 1654 로 나눠 봅시다.

234561이 됩니다.

엇?

뭔가 보인거 같은데, 한번 2345 | 61로 나눠 봅시다.

543216 입니다.

어어어엇???

보이십니까?

처음 수 : 123456

다음 : 321654 (거꾸로 하면 456123)

그 다음 : 234561

마지막 : 543216 (거꾸로 : 612345)

그렇습니다! 1~n까지가 환형으로 이어집니다!

그리고, 어짜피 w와 b가 교차되는 부분을 구하는 것이기 때문에, 거꾸로 하는 것도 결국 똑같이 계산해 줄 수 있다는 것을 알 수 있습니다!

그냥 처음에 입력되는 문자를 입력받아서, 가장 긴 길이를 출력하면 됩니다!

단! wbwb와 같은 글자는, 두 번 이으면 wbwbwbwb가 되고, 원래 글자가 4글자인데 반해, 총 길이가 8글자가 된다고 잘못 출력할 수 있습니다.

따라서, 만약 두 문자를 이어서 나온 길이가 처음 문자열보다 긴 경우에는 이를 잘 조절해주는 일을 해줍시다!

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//https://codeforces.com/contest/1025/problem/C
//Plasticine zebra
#pragma once
#include<cstdio>
#include<cstring>
int len;
char str[200001];
 
int main() {
    scanf("%s\n", str);
    len = strlen(str);
 
    for (int i = 0; i < len; i++) {
        str[len + i] = str[i];
    }
 
    char st = str[0];
    int cnt = 1;
    int res = 1;
    for (int i = 1; i < 2 * len; i++) {
        if (st != str[i]) {
            cnt++;
            res = res < cnt ? cnt : res;
        }
        else { cnt = 1; }
        st = str[i];
    }
    res = res > len ? len : res;
    printf("%d\n", res);
    return 0;    
}
Colored byㅁㅈㄹ  ㅈㄷ Color Scripter
cs

ㅇ

ㄴㅇㄹㅈㄷㄻㅈㄷㄹ

ㅅㅅ;

시간 복잡도

문자열을 한번 쭈욱 훑기 때문에 시간복잡도는 O(N)입니다.

Dima the hamster enjoys nibbling different things: cages, sticks, bad problemsetters and even trees!

Recently he found a binary search tree and instinctively nibbled all of its edges, hence messing up the vertices. Dima knows that if Andrew, who has been thoroughly assembling the tree for a long time, comes home and sees his creation demolished, he'll get extremely upset.

To not let that happen, Dima has to recover the binary search tree. Luckily, he noticed that any two vertices connected by a direct edge had their greatest common divisor value exceed $1$ .

Help Dima construct such a binary search tree or determine that it's impossible. The definition and properties of a binary search tree can be found here.

Input

The first line contains the number of vertices $n$ ( $2 \leq n \leq 700$ ).

The second line features $n$ distinct integers $a_{i}$ ( $2 \leq a_{i} \leq 10^{9}$ ) — the values of vertices in ascending order.

Output

If it is possible to reassemble the binary search tree, such that the greatest common divisor of any two vertices connected by the edge is greater than $1$ , print "Yes" (quotes for clarity).

Otherwise, print "No" (quotes for clarity).

Examples
inputCopy
6
3 6 9 18 36 108
outputCopy
Yes
inputCopy
2
7 17
outputCopy
No
inputCopy
9
4 8 10 12 15 18 33 44 81
outputCopy
Yes

Note

The picture below illustrates one of the possible trees for the first example.

$\text{[math]}$

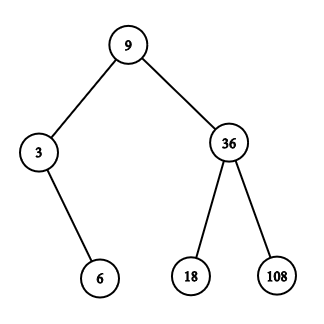
The picture below illustrates one of the possible trees for the third example.

$\text{[math]}$

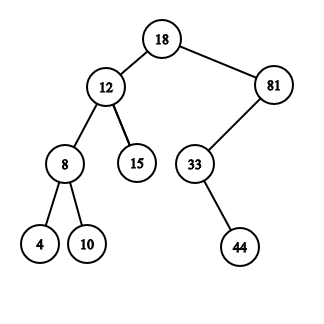
문제 해석

주어진 수들로 바이너리 서치 트리를 만들 수 있는지에 대한 문제입니다!

단, 주어진 수들이 부모, 자식간의 관계가 되기 위해서는 부모와 자식의 최대 공약수가 1이 넘어야 한다는 것입니다!

문제에서 주어지는 수는 오름차순으로 주어집니다!

어떻게 풀까?

이 문제는 바이너리 서치 트리의 특징을 이용한 문제라고 할 수 있습니다!

우선, 서로간에 부모 자식이 될 수 있는지 알기 위해서 노드들 간에 인접 행렬을 만들어야 합니다!

인접 행렬을 만드는 법은 간단하죠! 모든 노드 쌍을 보면서 구한 GCD의 값이 1이 아니라면 서로 부모와 자식이 될 수 있는 것입니다!

자, 이제 이렇게 부모와 자식이 될 수 있는 인접 행렬을 통해서 어떻게 바이너리 서치 트리를 만들 수 있는지 확인할 수 있을까요??

위 그림에서처럼 한 부모노드에서 왼쪽도 바이너리 서치 트리이고, 오른쪽도 바이너리 서치 트리여야 한다는 것이 바이너리 서치 트리의 특징입니다.

또한, 바이너리 서치 트리의 특성상, 큰 수는 모두 오른쪽에 위치하고, 작은 노드는 모두 왼쪽에 위치해야 합니다.

왼쪽 노드나 오른쪽 노드도 트리의 특성상 똑같은 바이너리 트리여야 하기 때문에, 부모와 똑같은 특징을 가집니다.

즉, 바이너리 서치 트리를 만들 수 있는가!? 에 대한 함수 make(l, r, mode)를 이용하면, 재귀적으로 트리를 만들 수 있는지 알아낼 수 있습니다!

그런데 함수에서 mode가 의미하는 것이 무엇일까요?

mode는 해당 노드가 왼쪽인지 오른쪽인지를 의미하는 말입니다!

왜 왼쪽에서 만들어지는지, 오른쪽에서 만들어지는지에 대한 정보가 필요한 것일까요?

만약, 27의 왼쪽 노드로 8~16의 값을 가지는 노드들을 바이너리 서치 트리로 만들면 만들 수 있습니다!

하지만, 7의 오른쪽 노드로 선택할 경우에는 8~14의 값을 가지는 노드들이 7과 1이 아닌 최대 공약수가 없기 때문에 트리를 만들 수 없습니다!

그리고, mode로 알 수 있는 것은 바로 해당 재귀 함수의 부모입니다.

만약, 해당 재귀함수가 어떤 노드의 왼쪽 노드라면, 해당 재귀함수의 부모는 당연히 r+1이 될 것입니다! 만약, r+1보다 더 높은 인덱스가 온다면, r+1번째 노드는 바이너리 서치 트리의 노드가 될 수 없기 때문이죠! 이것도 바이너리 서치 트리의 특징 덕분입니다!

따라서, mode를 이용하면, 해당 재귀함수의 부모를 구할 수 있습니다!

그럼, 이제 재귀 함수를 어떻게 구성하는지에 대해서 알아봅시다.

8~16의 값을 가지는 노드들을 트리로 만드느 경우 첫번째는 8을 자식으로 만들어 보는 것입니다.

두 번째는 10으로 자식을 만들어 보는 것이고,

다음은 12로 자식을 만들어 보는 경우고,

마지막으로 16을 자식으로 만들어 보는 것입니다.

즉, for문을 돌면서, l부터 r까지 보두 자식으로 만들어 보는 것입니다!

다만, 이렇게 되면, 시간복잡도가 굉장히 엄청나질 것입니다!

이를 해결한 방법이 없을까요!?

일단, 시간복잡도가 생기는 이유를 보면, 중복 계산이 엄청 많기 때문입니다!

1, 2, 3, 4, 5, 6, 7 의 노드가 있다고 합시다!

make(1,3,왼쪽)은 얼마나 불러질까요?

우선, 4를 맨 처음 루트로 삼을 때, 한번 불러질 것입니다!

그리고, 5를 루트로 만들 때에도,

4를 기준으로 make(1,3, 왼쪽)이 또 불러지겠죠.

이와 마찬가지로, 6을 ㄱ기준으로 만들 때에도,

4를 기준으로 이진트리를 만들고자 할 때, make(1,3,왼쪽)이 불러지고,

6에서 5를 기준으로 만들때, make(1,4, 왼쪽)가 호출되고,

이 안에서 또 4번을 기준으로 이진트리를 만들고자 할 때 make(1,3, 왼쪽)이 불러질 것입니다.

하지만, 생각해보면, make라는 함수에 l, r, mode만 들어간다면, 그 값이 변하지 않는다는 것을 알 수 있습니다.

따라서, 이를 메모이제이션을 통해서 관리합시다!

메모리에는 해당 memoi[l][r][mode]의 3차원 배열로 관리합시다!

해당 메모리에는 l, r, mode가 주어지면, 해당 make가 트리를 만들 수 있는지, 없는지를 반환합니다!

이렇게 하면, 그나마 중복 문제를 최선으로 해결할 수 있을 것입니다!

코드

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#pragma once
#include<cstdio>
#include<cstring>
using namespace std;
 
 
int gcd(int i1, int i2) {
    int r;
    if (i1 < i2) {
        int temp = i1;
        i1 = i2;
        i2 = temp;
    }
 
    while (i2) {
        r = i1 % i2;
        i1 = i2;
        i2 = r;
    }
 
    return i1;
}
 
int arr[701];
char canMake[3][701][701];
bool adj[701][701];
 
bool make(int p, int l, int r) {
    char &ret = canMake[p][l][r];
    if (l > r) return  ret = true;
    if (ret != -1) return ret;
    ret = 0;
    int parent;
    switch (p) {
    case 0:
        parent = 0;
        break;
    case 1:
        parent = r + 1;
        break;
    case 2:
        parent = l - 1;
        break;
    }
 
    for (int i = l; i <= r; i++) {
        if (adj[parent][i] && make(1, l, i - 1) && make(2, i + 1, r)) {
            return ret = 1;
        }
    }
 
    return ret;
}
 
int main() {
    int n;
    scanf("%d\n", &n);
    memset(canMake, -1, sizeof(canMake));
 
    for (int i = 1; i <= n; i++) {
        scanf("%d\n", &arr[i]);
    }
 
    for (int i = 1; i <= n; i++) {
        adj[0][i] = true;
 
        for (int j = i + 1; j <= n; j++) {
            if (gcd(arr[i], arr[j]) != 1) {
                adj[i][j] = true;
                adj[j][i] = true;
            }
        }
    }
 
    if (make(0,1, n)) {
        printf("Yes\n");
        return 0;
    }
    printf("No\n");
    return 0;
}
Colored by Color Scripter
cs

시간 복잡도

시간 복잡도는, 부분 문제가 이고,, 재귀에서 n번을 실행하기 때문에,이 됩니다! 굉장히 많은 시간복잡도를 가지는 군요!

여담

이번에는 실력이 모자란 코포였습니다. A번 밖에 맞지 못했지만, 다른 문제들에 대해서는 깔끔한 해결법도 찾지 못했던 것이 사실입니다!

다만, 이번에 잘 몰랐던 부분을 풀고 정리하면서 다음에 이런 문제가 나오면 잘 풀수 있도록 해야겠습니다.

'공부 > 알고리즘 문제풀이' 카테고리의 다른 글

[Codeforces] AIM Tech Round 5 (rated, Div. 1 + Div. 2) (0)	2018.08.31
[Codeforces] Codeforces Round #506 (Div. 3) (0)	2018.08.31
[Codeforces] Educational Codeforces Round 49 (Rated for Div. 2) (0)	2018.08.31
[Codeforces] Codeforces Round #504 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final) (0)	2018.08.30
[SW Expert Academy] 8월의 마지막 코드배틀 (0)	2018.08.29

비락 식혜를 낳는 블로그

[Codeforces] Codeforces Round #505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final)

'공부 > 알고리즘 문제풀이' 카테고리의 다른 글

티스토리툴바

[Codeforces] Codeforces Round #505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final)

'공부 > 알고리즘 문제풀이' 카테고리의 다른 글

'공부/알고리즘 문제풀이' Related Articles

티스토리툴바