드디어 제가 풀었던 코포들 중에 마지막 코포 정리입니다!
후후... 이 5번째 코포 풀이를 완성하면 왠지 떡상을 할 것 같은 좋은 느낌(?)이 듭니다. 후후후
Consider a table of size , initially fully white. Rows are numbered through from top to bottom, columns through from left to right. Some square inside the table with odd side length was painted black. Find the center of this square.
The first line contains two integers and () — the number of rows and the number of columns in the table.
The -th of the next lines contains a string of characters ( is 'W' for white cells and 'B' for black cells), describing the -th row of the table.
Output two integers and (, ) separated by a space — the row and column numbers of the center of the black square.
5 6
WWBBBW
WWBBBW
WWBBBW
WWWWWW
WWWWWW
2 4
3 3
WWW
BWW
WWW
2 1
문제 해석
요약을 많이 해드리겠습니다.
직사각형 B의 중심점의 위치를 출력하면 됩니다.
(단, 직사각형 B의 길이는 언제나 홀 수이기 때문에, 중앙점이 무조건 존재합니다.)
어떻게 풀까?
B는 직사각형이기 때문에, 왼쪽 위부터 한칸씩 보면, 연속되는 B의 가로와 세로의 위치를 구함으로써 가로와 세로의 길이를 구할 수 있습니다.
그리고, 중앙 위치는 맨 왼쪽 위의 B좌표 + 가로길이 / 2, 세로 길이 /2 지점이 되겠죠!
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 | #pragma once #include<cstdio> int n, m; char map[117][117]; struct cod { int r, c; }; cod findMID(int r, int c) { int nc = c; while (map[r][nc] == 'B') { nc++; } int nr = r; while (map[nr][c] == 'B') { nr++; } return { (nr + r) / 2, (c + nc) / 2 }; } int main() { scanf("%d %d\n", &n, &m); for (int i = 1; i <= n; i++) { scanf("%s\n", map[i]+1); } for (int i = 1; i <= n; i++) { for (int j = 1; j <= m; j++) { if (map[i][j] == 'B') { cod res = findMID(i, j); printf("%d %d\n", res.r, res.c); return 0; } } } return 0; } | cs |
Let be sum of digits in decimal representation of positive integer . Given two integers and , find some positive integers and such that
- ,
- ,
- .
The only line of input contain two integers and ().
Print two lines, one for decimal representation of and one for decimal representation of . Both numbers must not contain leading zeros and must have length no more than .
6 5
6
7
8 16
35
53
In the first sample, we have and . One valid solution is , . Indeed, we have and , and also .
문제 해석
에서 위 수를 빼면, 88888888888888..... 888889 라는 수가 나올 것입니다.
이 수를 s()함수에 넣으면 111111111...... 111111 보다 당연히 큰 수가 나올 것입니다.
즉, 어떤 경우에서든, 위 수를 출력하면 됩니다!
모든 조건에서 맞는 답을 구할 수 있는 것이죠!
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 | #pragma once #include<cstdio> #include<string> #include<iostream> using namespace std; int main() { string str[2]; int n, m; scanf("%d %d\n", &n, &m); for (int i = 0; i < 1129; i++) { str[0].push_back('1'); } for(int i = 0; i < 1128; i++) { str[1].push_back('8'); } str[1].push_back('9'); cout << str[0] << '\n'; cout << str[1] << '\n'; return 0; } | cs |
시간 복잡도
입력에 전혀 상관없기 때문에 O(1)입니다.
You are given rectangles on a plane with coordinates of their bottom left and upper right points. Some of the given rectangles have some common point. A point belongs to a rectangle if this point is strictly inside the rectangle or belongs to its boundary.
Find any point with integer coordinates that belongs to at least given rectangles.
The first line contains a single integer () — the number of given rectangles.
Each the next lines contains four integers , , and (, ) — the coordinates of the bottom left and upper right corners of a rectangle.
Print two integers and — the coordinates of any point that belongs to at least given rectangles.
3
0 0 1 1
1 1 2 2
3 0 4 1
1 1
3
0 0 1 1
0 1 1 2
1 0 2 1
1 1
4
0 0 5 5
0 0 4 4
1 1 4 4
1 1 4 4
1 1
5
0 0 10 8
1 2 6 7
2 3 5 6
3 4 4 5
8 1 9 2
3 4
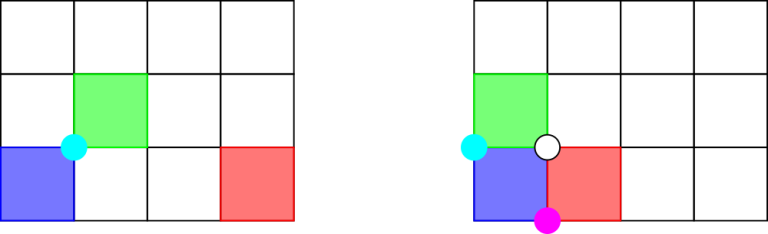
The picture below shows the rectangles in the first and second samples. The possible answers are highlighted.
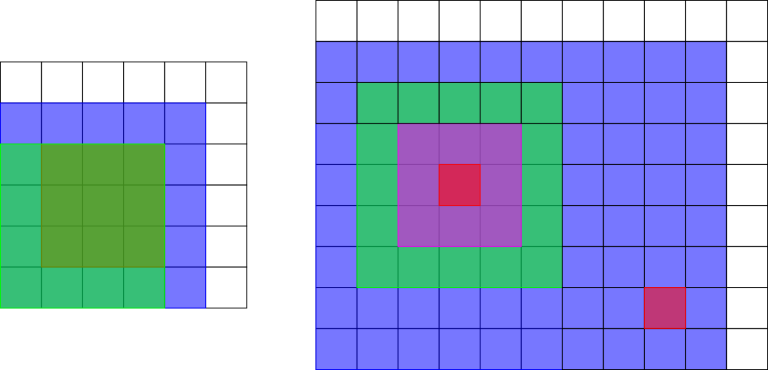
The picture below shows the rectangles in the third and fourth samples.
문제 해석
n개의 사각형이 주어집니다!
각 사각형은 왼쪽 아래 꼭지점의 (x, y)와 오른쪽 위 꼭지점 (x2, y2)로 주어집니다!
그리고 n개의 사각형 중에서 n-1개의 사각형이 공유하는 점이 있습니다!
이 때, n-1개의 사각형에 겹치는 점 하나 아무거나하나를 출력하세요!!
어떻게 풀까?
이번 문제도 이전에 코드포스에서 나왔던 구간 겹치기 문제와 유사합니다!
우선, 문제에 따르면, n-1개에 겹쳐지는 점은 무조건 존재합니다!
그러면, 점을 어떻게 구할 수 있을까요!?
이전 코드포스에서 풀었떤 최대 공통 구간의 길이를 구하는 것과 비슷합니다.
모든 사각형이 공유하는 점 이라는 것은, 시작점의 x좌표와 y좌표는 우선, 다른 사각형의 시작점의 x좌표와 y좌표보다 커야합니다!
가장 큰 시작점의 좌표가 xma, yma 라고 하겠습니다.
만약, 이 보다 작은 x, y 값을 선택하면,
xma와 yma는 해당 좌표를 포함하지 못하기 때문에 답이 될 수 없습니다!
또한, 이와 반대로 오른쪽 끝의 x좌표와 y좌표는 다른 사각형의 끝점 x좌표와 y좌표보다 작아야할 것입니다!
따라서, 시작점의 x좌표, 시작점의 y좌표, 끝 점의 x좌표, 끝 점의 y좌표를 정렬한 후에,
시작 점에서는 가장 큰 x좌표와 y좌표, 끝 점에서는 가장 작은 x좌표와 y좌표를 고르면 됩니다!
그리고, 또 하나의 조건이 있죠! 사각형의 특성상, 끝 점의 x좌표는 시작점의 x좌표보다 같거나 커야합니다!
마찬가지로 끝 점의 y좌표도 시작점의 y좌표보다 커야하죠!
위 조건을 만족하지 않는다면, 겹치지 않는 사각형 이라는 것이겠죠.
하지만, 이 문제에서의 조건은 n-1개의 사각형이 겹쳐야 한다는 것입니다!
하지만, 이 문제도 걱정할 것이 없습니다!
일단 1~n번째 사각형을 모두 순회하면서, 사각형을 하나씩 제거하는 경우를 보겠습니다.
i번째 사각형의 시작점의 x좌표를 xis, y좌표를 yis라고 하겠습니다.
끝점의 x좌표는 xie, y좌표는 yie라고 하죠!
만약, 정렬한 시작점 x의 좌표가 xis와 같다면 어떻게 해야할까요!?
해당 사각형의 점은 없어야 하기 때문에, 그 다음으로 큰 값을 가져오면 됩니다.
이는 나머지 세 점에 대해서도 모두 마찬가지이죠!
그리고 이렇게 고른 점 4개를 이용해서 위에서 봤던 사각형을 만들 수 있는가에 대한 판별식을 써서 만약 사각형이 될 수 있는 점 네 개라면,
둘 중에 아무거나 출력해주면 정답이 됩니다!!
코드
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 | #include<iostream> #include<algorithm> #include<tuple> #include<vector> using namespace std; typedef tuple<int, int, int,int> ti4; typedef vector<int> vi; ti4 rect[200000]; int main() { ios_base::sync_with_stdio(false); cin.tie(0); cout.tie(0); vi vl, vr, vd, vu; int l, r, d, u; int n; cin >> n; for (int i = 0; i < n; i++) { cin >> l >> d >> r >> u; vl.push_back(l); vd.push_back(d); vr.push_back(r); vu.push_back(u); rect[i] = { l,d,r,u }; } sort(vl.begin(), vl.end()); sort(vr.begin(), vr.end()); sort(vd.begin(), vd.end()); sort(vu.begin(), vu.end()); for (int i = 0; i < n; i++) { tie(l, d, r, u) = rect[i]; int xmin, xmax, ymin, ymax; xmin = l == *vl.rbegin() ? *next(vl.rbegin()) : *vl.rbegin(); xmax = r == *vr.begin() ? *next(vr.begin()) : *vr.begin(); ymin = d == *vd.rbegin() ? *next(vd.rbegin()) : *vd.rbegin(); ymax = u == *vu.begin() ? *next(vu.begin()) : *vu.begin(); if (xmin <= xmax && ymin <= ymax) { cout << xmin << ' ' << ymin << '\n'; return 0; } } return 0; } | cs |
시간 복잡도
시간 복잡도는 n개의 데이터를 정렬하기 위한 O(N log N)입니다!
여담
드디어.. 다 올렸습니다.... 기쁘다.. 좀쉬어야게써요
'공부 > 알고리즘 문제풀이' 카테고리의 다른 글
| [BOJ] 2206. 벽 부수고 이동하기 (0) | 2018.08.31 |
|---|---|
| [BOJ] 6603. 로또 (0) | 2018.08.31 |
| [Codeforces] Codeforces Round #506 (Div. 3) (0) | 2018.08.31 |
| [Codeforces] Codeforces Round #505 (rated, Div. 1 + Div. 2, based on VK Cup 2018 Final) (0) | 2018.08.31 |
| [Codeforces] Educational Codeforces Round 49 (Rated for Div. 2) (0) | 2018.08.31 |

